归并排序

发表于 | 分类于

算法思路

归并排序为 nlogn 时间复杂度的算法，是一种稳定的算法，大部分框架源码里面的排序算法都是采用归并排序。归并排序其实类似于二叉树的后序遍历。

归并排序的思路：

  1. 首先把数组分成 2 半，然后想办法把左边的数组排序，再想办法把右边的数组排序，之后再将它们归并起来
  2. 我们对左边和右边的数组进行排序的时候，再分别把左边和右边的数组分别分成一半，然后对每一个部分先排序再归并
  3. 对于 2 中的每一个部分，依然是先分半，再排序，后归并。
  4. 重复 3，当我们分到一定细度（每一部分只有 1 个数）的时候，没一个部分都是有序的。
  5. 逐步向上归并，当归并都最后一层的时候，就是有序数组了。

归并排序

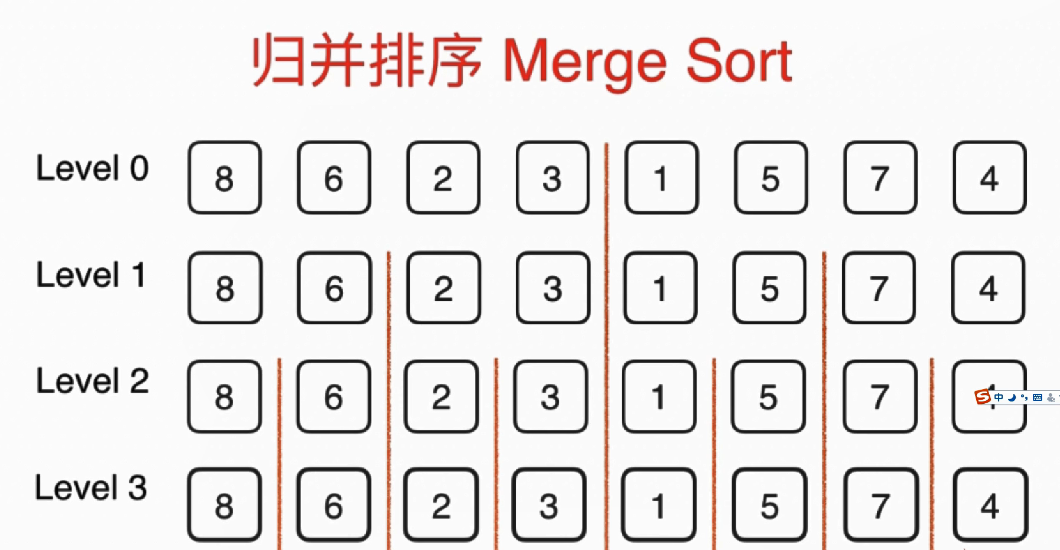
归并过程

  1. 先创建一个当前需要归并后结果数组一样长度的数组，并赋值
  2. 利用新创建数组中的 [0…mid] 与 [mid+1…r] 部分进行对比排序来对原数组赋值
  3. 这里用到双指针的方式对 l 和 mid+i 起始的两个索引进行维护

归并排序

实现的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
// 自顶向下的归并排序
	function mergeSort(arr, n) {
  __mergeSort(arr, 0, n - 1)
}
// 递归使用归并排序，对arr[l...r]的范围进行排序
function __mergeSort(arr, l, r) {
  if (l >= r) {
  	return
  }
  // if (r - l <= 15) { // 优化，当数组范围小于15位采用插入排序
  //     insertSort(arr, l, r);
  //     return;
  // }
  let mid = l + Math.floor((r - l) / 2) // 防止越界
  __mergeSort(arr, l, mid)
  __mergeSort(arr, mid + 1, r)
  if (arr[mid] > arr[mid + 1]) { // 还未有序则需要归并排序
  	__merge(arr, l, mid, r)
  }
}
// 将arr[l...mid]和arr[mid+1...r]两部分进行归并
function __merge(arr, l, mid, r) {
  // 拷贝一个新数组用于归并操作
  let auxArr = []
  for (let i = l; i <= r; i++) {
    auxArr[i-l] = arr[i]
  }
  // 归并, 利用 auxArr 值进行判断，对原数组 arr 进行赋值操作
  let n = l, m = mid + 1
  for (let k = l; k <= r; k++) {
  	if (n > mid) { // 如果 n 越界
      arr[k] = auxArr[m - l]
      m++
    } else if (m > r) { // 如果 m 越界
      arr[k] = auxArr[n - l]
      n++
    } else if (auxArr[n - l] < auxArr[m - l]) { // 没有越界的情况下判断
      arr[k] = auxArr[n - l]
      n++
    } else {
      arr[k] = auxArr[m - l]
      m++
    }
  }
}
// 对arr[l...r]范围内的数组进行插入排序
function insertSort (arr, l, r){
  for (let i = l+1; i <= r; i++) {
      let e = arr[i]
      let j
      for (j = i; j > l && arr[j-1] > e; j--) {
          arr[j] = arr[j-1]
      }
      arr[j] = e
  }
}

function mergeSortBU (arr, n) { // 自底向上的归并(还未优化)
  for (let sz = 1; sz <= n; sz += sz) { // 第一次看一个元素，第二次看两个元素，第三次看4个元素。。。每次加上自己
    for (let i = 0; i + sz < n; i += sz + sz) { // 对 [0 ~ sz-1] [sz ~ 2sz-1] [2sz ~ 3sz-1]。。。进行归并，i + sz < n 防止越界
      // 对 arr[i...i+sz-1] 和 arr[i+sz+sz-1] 进行归并
      let r = Math.min(i + sz + sz - 1, n - 1) // min取最小值防止越界
      if (arr[i + sz - 1] > arr[i + sz]) { // 还未有序则需要归并排序
		__merge(arr, i, i + sz - 1, r);
      }
    }
  }
}

let testArr = [5,1,6,4,3,8,2,7,10,9]
mergeSort(testArr, 10);
	console.log(testArr)
let testArr2 = [50,10,60,40,30,80,20,70,100,90]
mergeSortBU(testArr2, 10)
console.log(testArr2)

上面的说的归并排序主要是采用自顶向下的排序方式，在算法代码里，还涉及到了自低向上的归并排序，其过程是：

  1. 遍历所有元素，看一个元素，第二次看两个元素，第三次看4个元素。。。每次加上自己（加倍）
  2. 遍历 [0 ~ sz-1] [sz ~ 2sz-1] [2sz ~ 3sz-1]。。。进行归并，i + sz < n 判断用于防止越界
  3. 对 arr[i…i+sz-1] 和 arr[i+sz+sz-1] 进行归并

归并排序

以上就是归并排序的2种实现方法，这里记录以下方便查阅与复习