这里通过对比四种排序算法:插入排序,归并排序,快速排序和堆排序,来总结一下它们的使用场景和优缺点。
先上图:
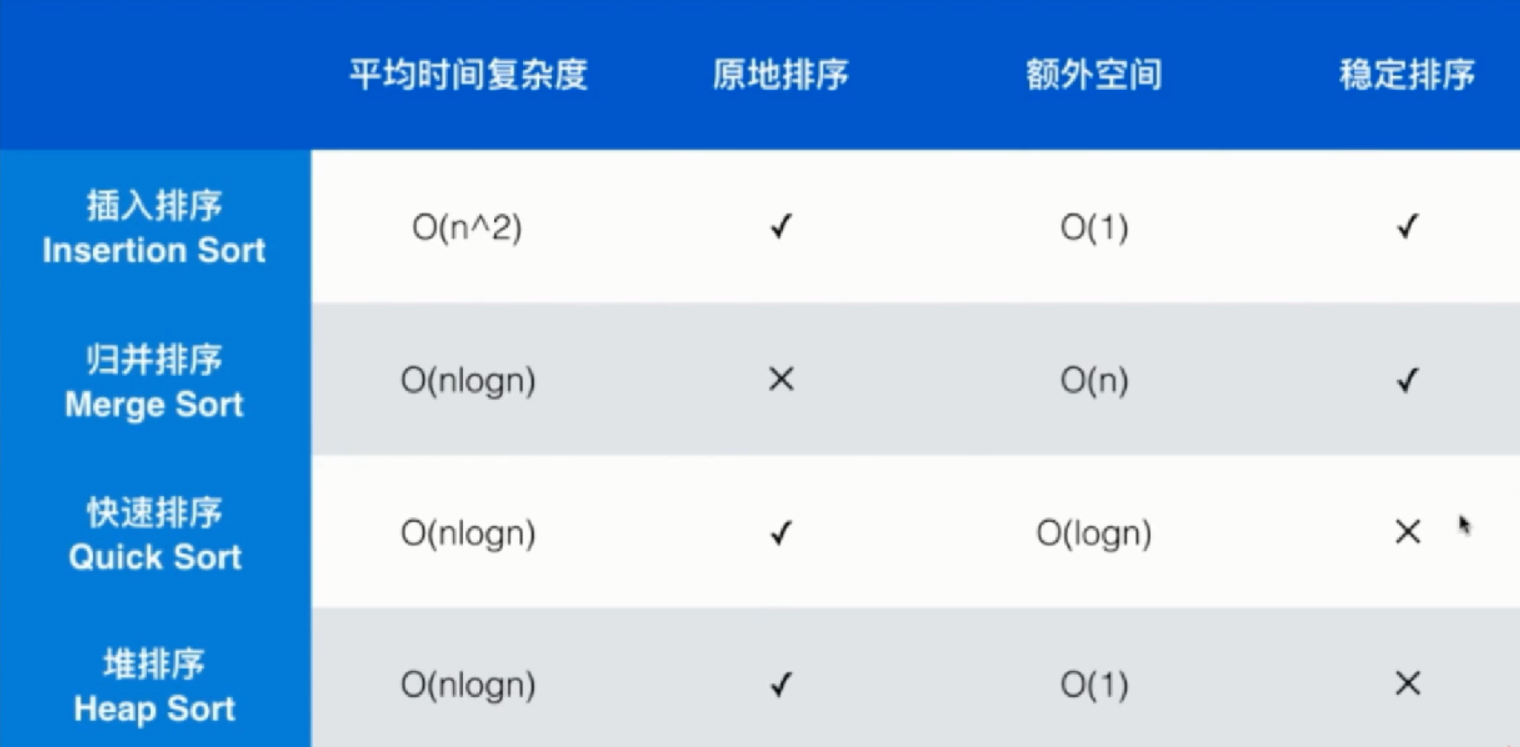
平均时间复杂度
从平均时间复杂度来看,只有插入排序是 O(n^2) 的时间复杂度,其他三种排序都是 O(nlogn) 的时间复杂度。
注意,这里说的是平均的时间复杂度,为什么要强调是平均时间复杂度呢?
大家应该知道,比如说对于插入排序,当我们要排序的数组已经是有序的情况下,那么插入排序算法就会退化到 O(n) 这个级别的时间复杂度。而对于快速排序算法,在极其特殊的情况下也会退化成 O(n^2) 级别的时间复杂度,我们一般会使用随机化的方式来尽量避免这个问题,使得快速排序算法退化成 O(n^2) 级别的时间复杂度的概率变得极其极其的小。
在通过前面的比较测试,可以发现:总体而言快速排序是更加快的排序算法。也就是说对于归并排序、快速排序和堆排序三个 O(nlogn) 时间复杂度的排序算法来说,它们也有常数上的差异,对于这个常数上的差异,快速排序相对占优。正因为如此,一般系统级别的排序都是使用快速排序来实现的。特别的对于有可能有大量的重复键值的情况下,使用的是三路快速排序。
是否是原地排序
大家可以发现,插入排序、快速排序和堆排序这三种排序都可以都过直接在数组上交换元素进而完成排序,而归并排序却不可以。归并排序必须开辟而外的空间来完成归并的过程,才能完成归并排序。
正因为如此,如果一个系统对空间相对比较敏感的话,那么归并排序可能就并不适合。
额外空间
对于插入排序和堆排序来说,它们都可以直接在数组上通过交换元素的位置来来完成,所以它们所用的额外空间是 O(1) 级别的,也就是常数级别的空间。不管你要排序的数组有多少个变量,我之需要开辟几个临时的变量就能完成这个排序了。
而归并排序它需要 O(n) 的额外的空间,来完成归并的过程。
这里需要注意,快速排序需要的额外空间是 O(logn) 的,为什么是 logn 呢?
因为对于快速排序来说,我们采用递归的方式来进行排序,那么这个递归过程一共有 logn 这么多层,这么多层的递归就需要有相应的 logn 层的栈空间来保存每一次递归过程中的临时变量,以供递归返回的时候继续使用。为此大家需要注意,快速排序虽然是原地排序,但是它所耗费的空间是 logn 这个级别的。
是否是稳定排序
先说结论:插入排序和归并排序属于稳定排序,快速排序和堆排序不属于稳定的排序。
什么是排序算法的稳定性?
稳定排序就是:对于相等的元素,在排序后,原来靠前的元素依然靠前,即相等元素的相对位置没有发生改变。
例如:

这里通过不同的颜色标记了排序前的 “3” 和排序后的 “3” 的顺序,可以发现三个 “3” 的相对位置是没有改变的。
这里需要注意的是,虽然插入排序和归并排序是属于稳定排序,但是不同的实现方式可能变成不稳定排序,书所以写的时候需要注意实现方式。
除了在需求需要稳定排序的时候直接采用稳定排序算法,我们也可以通过自定义比较函数,让排序算法不存在稳定性的问题,比如说:
1 | bool operator<(const Student& otherStudent){ |
在判断两个学生之间的大小关系的时候,这两个学生他们的分数是不是相同,如果不相等就按分数排序,如果相等就看名字的字符串的大小关系。
使用这样的方式,在比较中相当于多比较了一下,正因为如此,效率有所损耗。不过在一般的情况下使用现代的计算机,这个损耗完全可以承受的,只是在一些对于性能非常敏感的情况下,或者说对于这种比较的函数不太好更改的情况下,我们又希望排序的结果是具有稳定性。那么稳定的排序就具有了意义。
所以通常在系统级别的类库中,我们需要实现一个稳定的排序,通常选择的归并排序这个算法。
这里只比较了这四种排序,还有很多排序也可以拿来通过这四种指标进行一下总结对比。